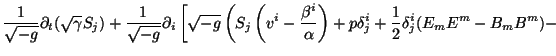Electromagnetic fields in curved spacetimes.
Accurate description of astrophysical phenomena near black hole
should take into account general relativistic effects. In particular, an
important issue that has not received enough attention in the past due
to its great complexity is the evolution of electromagnetic fields in curved
spacetimes.
The conservation equation for the particle number in a single component
perfect fluid can be written in covariant form:
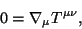 |
(1) |
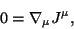 |
(2) |
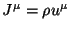 ,
,
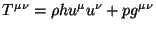 ,
,
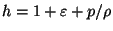 is the relativistic enthalpy,
is the relativistic enthalpy, 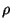 is the density,
is the density, 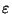 is the internal energy,
is the internal energy, 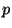 is the pressure; an equation of state (EOS) is needed and there are two
EOS that are often used: the polytropic EOS
is the pressure; an equation of state (EOS) is needed and there are two
EOS that are often used: the polytropic EOS 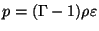 ,
and the relativistic EOS:
,
and the relativistic EOS: 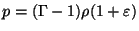 ,
where
,
where 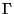 is the polytropic coefficient of the fluid.
is the polytropic coefficient of the fluid.
Following the 3+1 formalism and the Valencia formalism, the metric is
written as:
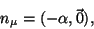 |
(3) |
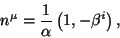 |
(4) |
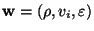 :
:
where 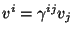 are the contravariant components of the Eulerian observers,
are the contravariant components of the Eulerian observers,
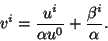 |
(8) |
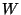 is the Lorentz relativistic factor,
is the Lorentz relativistic factor, 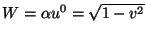 ,
, 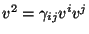 .
The eqs. (0.1-0.2)
can now be rewritten as a conservative first order system:
.
The eqs. (0.1-0.2)
can now be rewritten as a conservative first order system:
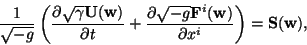 |
(9) |
 denotes the transpose):
denotes the transpose):
![\begin{displaymath}\mathbf{U(w^i)} = [D,S_j,\tau]^T,\end{displaymath}](img29.gif) |
(10) |
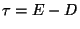 ;
the flux vector is:
;
the flux vector is:
![\begin{displaymath}{\bf F}^i({\bf w}) = \left[D\left( v^i-\frac{\beta^i}{\alp...... \left( v^i-\frac{\beta^i}{\alpha} \right) + p v^i\right]^T,\end{displaymath}](img31.gif) |
(11) |
![\begin{displaymath}{\bf S(w)} = \left[0,T^{\mu\nu}\left( \frac{\partial g_{...... x^{\mu}}-T^{\mu\nu} \Gamma^{0}_{\nu\mu} \right)\right]^T.\end{displaymath}](img32.gif) |
(12) |
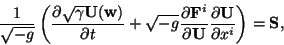 |
(13) |
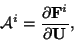 |
(14) |
where 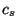 is the local speed of sound,
is the local speed of sound, 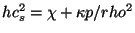 ,
with
,
with 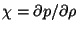 and
and 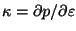 .
A complete set of eigenvectors is:
.
A complete set of eigenvectors is:
with
and 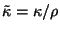 ,
, 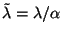 ,
, 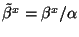 .
.
The eqs.(0.9) can be discretized
as (assuming one dimension for simplicity):
![\begin{displaymath}\frac{1}{\sqrt{-g}}\frac{\partial \sqrt{\gamma}{\bf U}_i}{\p......c{(f^*)_{i+1/2}-(f^*)_{i-1/2}}{\Delta x} \right]+ {\bf S}_i,\end{displaymath}](img58.gif) |
(23) |
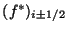 is the ``numerical flux'' computed at the interfaces
is the ``numerical flux'' computed at the interfaces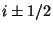 of the spatial cell
of the spatial cell 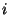 ,
and is given by:
,
and is given by:
![\begin{displaymath}(f^*)_{i+1/2} = \frac{1}{2}\left[ {\bf F}^R + {\bf F}^L -\......mbda_m\right\vert\Delta\tilde\omega_m\tilde {\bf r}_m \right],\end{displaymath}](img62.gif) |
(24) |
 y
y 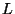 are the right and left interfaces of one cell, and
are the right and left interfaces of one cell, and 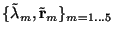 are the eigenvalues and eigenvectors at the cell interface using the average
of the primitive variables. Finally,
are the eigenvalues and eigenvectors at the cell interface using the average
of the primitive variables. Finally, 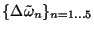 are the jumps in the characteristic variables, given by:
are the jumps in the characteristic variables, given by:
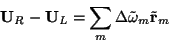 |
(25) |
plus the conservation of electric charge:
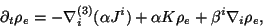 |
(30) |
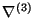 is the covariant derivative with respect to the spatial metric
is the covariant derivative with respect to the spatial metric 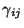 ,
, 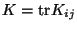 is the trace of the extrinsic curvature,
is the trace of the extrinsic curvature, 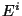 and
and 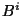 are the electric and magnetic fields as measured by an Eulerian observer,
and
are the electric and magnetic fields as measured by an Eulerian observer,
and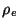 is the electric charge density.
is the electric charge density.
The conservation of the new energy-momentum tensor gives:
where we have redefined the energy density:
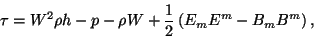 |
(35) |
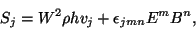 |
(36) |
Hugo Villegas
2002-01-22
![]() ,
,
![]() ,
,
![]() is the relativistic enthalpy,
is the relativistic enthalpy, ![]() is the density,
is the density, ![]() is the internal energy,
is the internal energy, ![]() is the pressure; an equation of state (EOS) is needed and there are two
EOS that are often used: the polytropic EOS
is the pressure; an equation of state (EOS) is needed and there are two
EOS that are often used: the polytropic EOS ![]() ,
and the relativistic EOS:
,
and the relativistic EOS: ![]() ,
where
,
where ![]() is the polytropic coefficient of the fluid.
is the polytropic coefficient of the fluid.
![]() are the contravariant components of the Eulerian observers,
are the contravariant components of the Eulerian observers,
![]() is the local speed of sound,
is the local speed of sound, ![]() ,
with
,
with ![]() and
and ![]() .
A complete set of eigenvectors is:
.
A complete set of eigenvectors is:
![$\displaystyle \left[\frac{{\cal K}}{hW},v_x,v_y,v_z,1-\frac{{\cal K}}{hW}\right]^T,$](img44.gif)
![$\displaystyle \left[1,hW\left(v^x-\frac{v^x-\Lambda^x_{\pm}}{\gamma^{xx}-v^x\L......hW\frac{\gamma^{xx}-v^xv^x}{\gamma^{xx}-v^x\Lambda^x_{\pm}}\right)-1\right]^T,$](img50.gif)
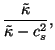
![]() ,
, ![]() ,
, ![]() .
.
![\begin{displaymath}(f^*)_{i+1/2} = \frac{1}{2}\left[ {\bf F}^R + {\bf F}^L -\......mbda_m\right\vert\Delta\tilde\omega_m\tilde {\bf r}_m \right],\end{displaymath}](img62.gif)
![$\displaystyle \frac{1}{\sqrt{-g}}\partial_{t}(\sqrt{\gamma}\tau)+\frac{1}{\sqrt......c{1}{2}(E_{m}E^{m}-B_{m}B^{m}) \right)v^i + \epsilon^{ijk}E_{j}B_{k} \right] -$](img84.gif)