Critical Phenomena in Gravitational Collapse

Critical phenomena in gravitational collapse were discovered by Choptuik in 1993 in the spherically symmetric collapse of massless scalar field. Since then the phenomenon has been observed in a variety of matter sources. At the threshold of gravitational collapse the matter is just about to form a black hole and an infinitesimally small perturbation can either cause the matter to disperse to infinity or to form a black hole. The dynamics close to the threshold exhibits interesting behaviour such as power law scaling of length scales, self similarity of the solutions and universaity. 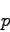A typical setup is to take an initial matter distribution parametrized by a single parameter \begin{displaymath}p\end{displaymath} . 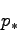Then one performs a bisection search to determine the critical value \begin{displaymath}p_*\end{displaymath} . The critical exponent can be determined from the scaling relation of the black hole mass

\begin{displaymath}M_{\rm bh} \sim \vert p-p_*\vert^\gamma\end{displaymath}
or, more conveniently, from the scaling relation of the maximum of the scalar curvature
\begin{displaymath}R_{\rm max} \sim \vert p-p_*\vert^{-2\gamma}\end{displaymath}

To numerically evolve near critical solutions is a non-trivial task. The critical solution is self-similar, i.e., it repeats itself on ever decreasing length scales. The fluid density and pressure increase by many order of magnitudes and in some cases the fluid velocity becomes extremely relativistic.
Critical collapse is a very good starting point for getting acquinted with advanced numerical techniques such as adaptive mesh refinment (AMR). A widely studied matter model is the ultrarelativistic limit of ideal fluid with the equation of state
\begin{displaymath}P = (\Gamma-1)\rho\end{displaymath}
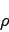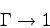where \begin{displaymath}\rho\end{displaymath} is the total energy density of the fluid. I was in particularly interested in the limit of \begin{displaymath}\Gamma\to 1\end{displaymath} in which the fluid becomes dust-like. The dust limit is interesting to study since it has been conjectured that the scaling exponent for dust should assume some simple value such as 1. 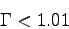Also there have been claims of naked singularity formation in ideal fluid collapse for \begin{displaymath}\Gamma < 1.01\end{displaymath} . Another way of investigating the critical collapse is to use the fact that the critical solution is continuously selfsimilar. By using the selfsimilar ansatz the set of PDEs transform into a set of ODEs that can then be solved quite easily numerically to a very high precision (therefore I will call it exact). One then performs a perturbation analysis around the critical solution to determine the scaling exponent.
\begin{displaymath}ds^2=-\alpha(r)^2 dt^2+a(r)^2 dr^2 + r^2(d\theta^2+\sin^2\theta\, d\phi^2)\end{displaymath}
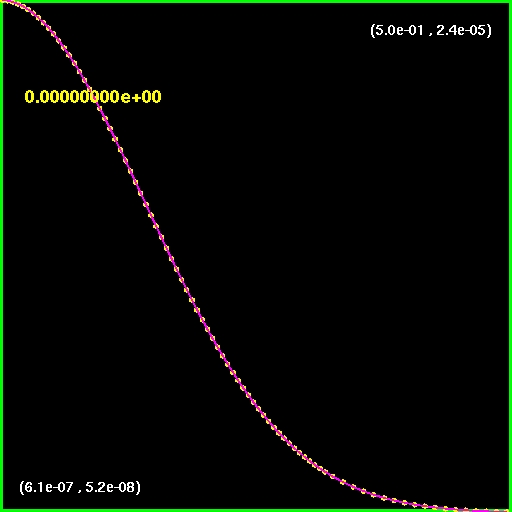
\begin{displaymath}r\end{displaymath} Below are some results from the numerical calculations. For the numerical simulations we used spherical polar coordinates with the metric element The first image/movie shows the initial profile of the fluid density. The evolution can be seen by clicking on the image. The evolution is shown in the standard coordinate. Also note that the magnitude increases by a factor of 107. 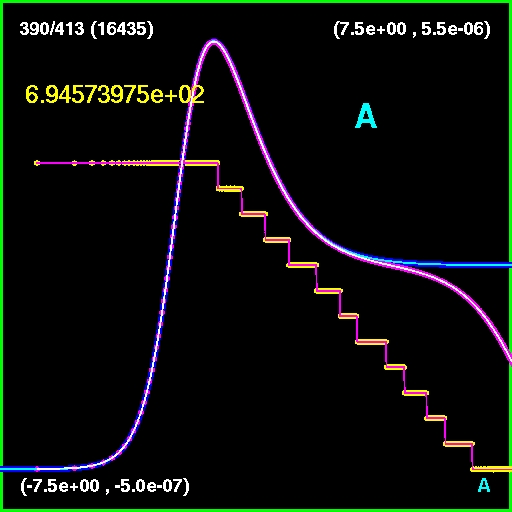The second image shows a near-critical solution of \begin{displaymath}a\end{displaymath} compared with the exact one. This image and the movie are shown in self similar coordinates. The stairs-like line represents a grid hierarchy level. At each successive hierarchy level the distance between two neighbouting points is reduced by a factor of two. The grid hierarchy is adjusted whenever certain criteria are not met. In that case the calculation starts from a previous (successful) checkpoint with adjusted grid structure. This scheme assures that our preset criteria are satisfied during the entire evolution.
Note that the numerical and exact solutions match only in a limited region and have very different behaviour asymptotically. This is due to the fact that the exact solution represents spacetime that is not asymptotically flat, whereas in the numerical calculations there is only a finite amount of matter and the resulting spacetime is asymptotically flat. However, the scaling exponent only depends on the behaviour near to the origin where the both solution match. 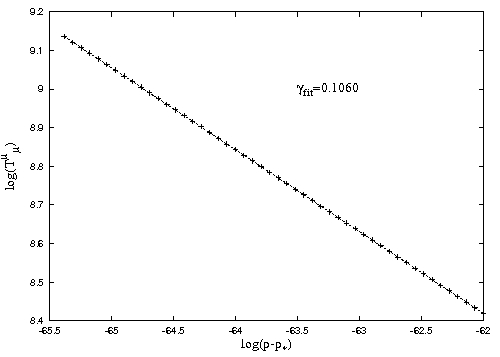The last image shows data points obtained from numerical simulations together with the linear fit and the value of the scaling exponent. More details can be found in the paper Critical Colapse of an Ultrarelativistic Fluid in the 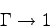\begin{displaymath}\Gamma\to 1\end{displaymath} Limit (gr-qc/0508062)
Initial density profile of the fluid density in standard spherical polar coordinate \begin{displaymath}r\end{displaymath} .
(click to play mpeg movie) 		Comparison of the numerical and exact critical solutions of \begin{displaymath}a\end{displaymath} in self-similar coordinates.
The hierarchy levels are also shown.
(click to play mpeg movie)


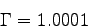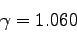
Data obtained from subcritical runs for \begin{displaymath}\Gamma = 1.0001\end{displaymath} . The line represents the best linear fit to the data. The value of the scaling exponent obtained from the linear fit is \begin{displaymath}\gamma = 1.060\end{displaymath}