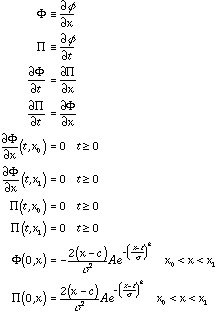New Features in RNPL

April 9, 1998

Robert Marsa





Overview




 

 




Compiler Command-line Features




 

  • Parallelism
    • Trivial
    • DAGH



  • Languages
    • c
    • c++
    • f77
    • f90
    • allf
    • upf
    • idf

  • Files
    • updates
    • initializers
    • residuals



Parameters

 

  • New Parameters
    • epsiterid
    • maxstepid
    • trace


  • Command-line
    wave -p "amp:=1.0e-3"
    wave -p 'in_file:="myfile.state"'

  • Parallel
    wave -v "amp:=1.0e-3-1.0e-4/100"
    wave -v "delta:=1.0,2.0,3.0-4.0/10"

  • Ordering and Fetching
    • Command-line
    • Parameter file
    • Attribute file
    • State file
    • Default




Attributes


 

  • Default Values
    attribute int out_gf encodeone := [1]
    attribute int out_gf encodeone := [0]
    old-style
    attribute int out_gf encodeone := [ 1 1 1 1 1 ]




  • Embedded Definitions
    float u on grid1 at -1,0,1 { out_gf:=1 }
    float v on grid1 at -1,0,1 { out_gf[res]:=1 }

    attribute int fl encodeall := [0]
    float u on g1 at 0,1 { out_gf:=1,fl:=1 }
    float v on g1 at 0,1 { fl[res]:=1,fl[0]:=1 }



Functions and Operators

 

 




Initializations


Multiple Time Levels

initialize phi { [1:Nx] := A*exp(-(x-c)^2/sigma^2) }
initialize <-1>phi {
[1:1] := 0;
[2:Nx-1] := 0.5*(dt/dx)^2*(<0>phi[1] + <0>phi[-1]) +
(1-(dt/dx)^2)*phi -
dt*2*(x-c)/sigma^2*phi;
[Nx:Nx] := 0
}

Initializers

auto initialize phi,Phi,Pi

init.frag init initialize
Ktt, Krr, a, beta, dmdr, mass
header
Phi, Pi, Ktt, Krr, a, beta, dmdr, mass, r, dr, PI, M

auto initialize ah,R,mass2,hc,mc,Ricci

Issues




Future Additions


 

 

Examples



2nd Order Wave Equation










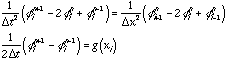
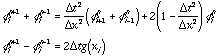
# Sample program for 98/04/09 Relativity Seminar
# This program solves 1D 2nd order wave equation
# phi_tt = phi_xx (string with endpoints fixed)

parameter float xmin := 0
parameter float xmax := 100
parameter float A := 1.0
parameter float c
parameter float sigma

rect coordinates t,x

uniform rect grid g1 [1:Nx] {xmin:xmax}

float phi on g1 at -1,0,1 { out_gf := 1 }

operator D_LF(f,x,x) := (<0>f[1] - 2*<0>f[0] + <0>f[-1])/(dx*dx)
operator D_LF(f,t,t) := (<1>f[0] - 2*<0>f[0] + <-1>f[0])/(dt*dt)
operator D_LF(f,x) := (<0>f[1] - <0>f[-1])/(2*dx)
operator D_LF(f,t) := (<1>f[0] - <-1>f[0])/(2*dt)

evaluate residual phi { [1:1] := D_LF(phi,t);
[2:Nx-1] := D_LF(phi,t,t) - D_LF(phi,x,x);
[Nx:Nx] := D_LF(phi,t) }

initialize phi { [1:Nx] := A*exp(-(x-c)^2/sigma^2) }
initialize <-1>phi {
[1:1] := 0;
[2:Nx-1] := 0.5*(dt/dx)^2*(<0>phi[1] + <0>phi[-1]) +
(1-(dt/dx)^2)*phi -
dt*2*(x-c)/sigma^2*phi;
[Nx:Nx] := 0
}

looper iterative

auto update phi


1st Order Wave Equation



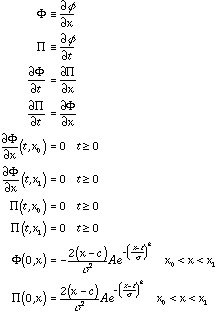
# Sample program for 98/04/09 Relativity Seminar
# This program solves 1D 1st order wave equation
# phi_tt = phi_xx (string with endpoints fixed)
# Phi_t=Pi_x
# Pi_t=Phi_x

parameter float xmin := 0
parameter float xmax := 100
parameter float A := 1.0
parameter float c
parameter float sigma

rect coordinates t,x

uniform rect grid g1 [1:Nx] {xmin:xmax}

float phi on g1 at 0,1 { out_gf := 1 }
float Phi on g1 at -1,0,1 { out_gf := 1 }
float Pi on g1 at -1,0,1 { out_gf := 1 }

operator D_FW(f,x) := (-3*<1>f[0] + 4*<1>f[1] - <1>f[2])/(2*dx)
operator D_BW(f,x) := (3*<1>f[0] - 4*<1>f[-1] + <1>f[-2])/(2*dx)
operator D_LF(f,x) := (<0>f[1] - <0>f[-1])/(2*dx)
operator D_LF(f,t) := (<1>f[0] - <-1>f[0])/(2*dt)
operator D_CN(f,t) := (<1>f[0] - <0>f[0])/dt
operator AVG(f,t) := (<1>f[0]+<0>f[0])/2

evaluate residual Pi {
[1:1] := D_LF(Pi,t);
[2:Nx-1] := D_LF(Pi,t) = D_LF(Phi,x);
[Nx:Nx] := D_LF(Pi,t)
}

evaluate residual Phi {
[1:1] := D_FW(Phi,x);
[2:Nx-1] := D_LF(Phi,t) = D_LF(Pi,x);
[Nx:Nx] := D_BW(Phi,x)
}

residual phi {
[1:Nx] := D_CN(phi,t) = AVG(Pi,t)
}

initialize phi { [1:Nx] := A*exp(-(x-c)^2/sigma^2) }
initialize Phi { [1:Nx] := -2*(x-c)/sigma^2*phi }
initialize Pi { [1:Nx] := 2*(x-c)/sigma^2*phi }

looper iterative

auto update Phi,Pi,phi


Einstein-Klein-Gordon Equation
in Ingoing Eddington-Finkelstein Coordinates







# Sample program for 98/04/09 Relativity Seminar
# This program solves Einstein's equation coupled to a scalar field
# in ingoing Eddington-Finkelstein coordinates
# Note: shown here is only a part of this program

parameter float PI := 3.14159265358979
parameter float rmin := 2.0
parameter float rmax
parameter float epsdis
parameter float M
parameter float cent
parameter float amp
parameter float sigma
parameter int d := 2
parameter float bhthresh := 1.1

attribute int out_gf encodeone := [ 0 ]

sph coordinates t,r
uniform sph grid g1 [0:Nr-1] {rmin:rmax}

float phi on g1 at 0,1
float Phi on g1 at 0,1 { out_gf := 1 }
float Pi on g1 at 0,1
float a on g1 at 0,1 { out_gf := 1 }
float Ktt on g1 at 0,1 { out_gf := 1 }
float Krr on g1 at 0,1
float beta on g1 at 0,1
float dmdr on g1 { out_gf := 1 }
float mass on g1 { out_gf := 1 }
float ah on g1
float mc on g1
float hc on g1
float mass2 on g1
float R on g1
float Ricci on g1

evaluate residual Phi {
[0:0] := if(R != 0) then
D_CN(Phi,t) = D_FWA(beta*Phi + (1-beta)*Pi,r)
else D_CN(Phi,t);
[1:1] := if(R != 0 && <0>R[-1] != 0) then
D_CN(Phi,t) = D_AN(beta*Phi + (1-beta)*Pi,r)
else if(R != 0) then
D_CN(Phi,t) = D_FWA(beta*Phi + (1-beta)*Pi,r)
else D_CN(Phi,t);
[2:Nr-3] := if(R != 0 && <0>R[-1] != 0 && <0>R[-2] != 0) then
D_CND(Phi,t) = D_AN(beta*Phi + (1-beta)*Pi,r)
else if(R !=0 && <0>R[-1] != 0) then
D_CN(Phi,t) = D_AN(beta*Phi + (1-beta)*Pi,r)
else if(R != 0) then
D_CN(Phi,t) = D_FWA(beta*Phi + (1-beta)*Pi,r)
else D_CN(Phi,t);
[Nr-2:Nr-2] := D_CN(Phi,t) = D_AN(beta*Phi + (1-beta)*Pi,r);
[Nr-1:Nr-1] := D_CN(Phi,t) + (1-2*AVG(beta,t))*D_BWA(Phi,r) +
(1-2*AVG(beta,t)-2*r*D_BWA(beta,r))*AVG(Phi,t)/r -
(1-2*AVG(beta,t)+2*r*D_BWA(beta,r))*AVG(phi,t)/(r^2)
}

residual Pi {
[0:0] := if(R != 0) then
D_CN(Pi,t) = 1/(r^2)*D_FWA(r^2*(beta*Pi + (1-beta)*Phi),r);
[1:1] := if(R != 0 && <0>R[-1] != 0) then
D_CN(Pi,t) = 1/(r^2)*D_AN(r^2*(beta*Pi + (1-beta)*Phi),r)
else if(R != 0) then
D_CN(Pi,t) = 1/(r^2)*D_FWA(r^2*(beta*Pi + (1-beta)*Phi),r);
[2:Nr-3] := if(R != 0 && <0>R[-1] != 0 && <0>R[-2] != 0) then
D_CND(Pi,t) = 1/(r^2)*D_AN(r^2*(beta*Pi + (1-beta)*Phi),r)
else if(R != 0 && <0>R[-1] != 0) then
D_CN(Pi,t) = 1/(r^2)*D_AN(r^2*(beta*Pi + (1-beta)*Phi),r)
else if(R != 0) then
D_CN(Pi,t) = 1/(r^2)*D_FWA(r^2*(beta*Pi + (1-beta)*Phi),r);
[Nr-2:Nr-2] := D_CN(Pi,t) = 1/(r^2)*D_AN(r^2*(beta*Pi + (1-beta)*Phi),r) ;
[Nr-1:Nr-1] := (1-AVG(beta,t))*AVG((Pi+Phi),t) + (1-2*AVG(beta,t))*AVG(phi,t)/r
}

evaluate residual Ktt {
[0:0] := if(R != 0) then
D_CN(Ktt,t) = AVG(beta,t)*D_FWA(Ktt,r) +
D_FWA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t)
else D_CN(Ktt,t);
[1:1] := if(R != 0 && <0>R[-1] != 0) then
D_CN(Ktt,t) = AVG(beta,t)*D_AN(Ktt,r) +
D_LFA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t)
else if(R != 0) then
D_CN(Ktt,t) = AVG(beta,t)*D_FWA(Ktt,r) +
D_FWA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t)
else D_CN(Ktt,t);
[2:Nr-3] := if(R != 0 && <0>R[-1] != 0 && <0>R[-2] != 0) then
D_CND(Ktt,t) = AVG(beta,t)*D_AN(Ktt,r) +
D_LFA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t)
else if(R != 0 && <0>R[-1] != 0) then
D_CN(Ktt,t) = AVG(beta,t)*D_AN(Ktt,r) +
D_LFA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t)
else if(R != 0) then
D_CN(Ktt,t) = AVG(beta,t)*D_FWA(Ktt,r) +
D_FWA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t)
else D_CN(Ktt,t);
[Nr-2:Nr-2] := D_CN(Ktt,t) = AVG(beta,t)*D_AN(Ktt,r) +
D_LFA(beta,r)/(AVG(a,t)*r) +
(1-AVG(beta,t))*(AVG(a,t) - 1/AVG(a,t))/(r^2) +
AVG(a,t)*(1-AVG(beta,t))*AVG(Ktt,t)*AVG((2*Ktt+Krr),t);
[Nr-1:Nr-1] := <1>Ktt[0]=<1>beta[0]/(r*<1>a[0]*(1-<1>beta[0])) }

residual a {
[0:0] := if(R != 0) then
D_CN(a,t) = D_FWA(a*beta,r) - (AVG(a,t)^2)*(1-
AVG(beta,t))*AVG(Krr,t);
[1:1] := if(R != 0 && <0>R[-1] != 0) then
D_CN(a,t) = D_AN(a*beta,r) - (AVG(a,t)^2)*(1-AVG(beta,t))*AVG(Krr,t)
else if(R != 0) then
D_CN(a,t) = D_FWA(a*beta,r) - (AVG(a,t)^2)*(1-
AVG(beta,t))*AVG(Krr,t);
[2:Nr-3] := if(R != 0 && <0>R[-1] != 0 && <0>R[-2] != 0) then
D_CND(a,t) = D_AN(a*beta,r) - (AVG(a,t)^2)*(1-AVG(beta,t))*AVG(Krr,t)
else if(R != 0 && <0>R[-1] != 0) then
D_CN(a,t) = D_AN(a*beta,r) - (AVG(a,t)^2)*(1-AVG(beta,t))*AVG(Krr,t)
else if(R != 0) then
D_CN(a,t) = D_FWA(a*beta,r) - (AVG(a,t)^2)*(1-
AVG(beta,t))*AVG(Krr,t);
[Nr-2:Nr-2] := D_CN(a,t) = D_AN(a*beta,r) - (AVG(a,t)^2)*(1-AVG(beta,t))*AVG(Krr,t);
[Nr-1:Nr-1] := <1>a[0] = exp(PI/4*(r^2-P0(r,r)^2)*(<1>phi[0]/r + P0(phi/r,r))^2)*
sqrt(P0(a,r)^2*(1-P0(beta,r))*(2 -
P0(r,r)*(1-2*P0(beta,r))/(r*(1-P0(beta,r))) -
(r-P0(r,r))/r*P0(a,r)^2*(1-P0(beta,r))*
exp(PI/4*(r^2-P0(r,r)^2)*(<1>phi[0]/r + P0(phi/r,r))^2))
)
}

residual <1>[0]dmdr { [0:0] := if(R != 0) then
dmdr = 4*PI*r^2*((Phi^2+Pi^2)/(2*a^2) + r*Ktt*Phi*Pi/a);
[1:Nr-1] := if(R != 0 && <0>R[-1] != 0) then
dmdr = 4*PI*r^2*((Phi^2+Pi^2)/(2*a^2) + r*Ktt*Phi*Pi/a)
else if(R != 0) then
dmdr = 4*PI*r^2*((Phi^2+Pi^2)/(2*a^2) + r*Ktt*Phi*Pi/a) }

residual <1>[0]mass { [0:0] := if(R != 0) then
mass = r/2;
[1:Nr-1] := if(R != 0 && <0>R[-1] != 0) then
D_BW(mass,r) = AVG(dmdr,r)
else if(R != 0) then
mass = r/2 }

residual <1>[0]ah { [0:Nr-1] := if(R != 0) then ah = a*r*Ktt }

residual R { [Nr-1:Nr-1] := R = 1;
[Nr-2:1:-1] := if(ah > bhthresh || <0>R[1]==0) then
R = 0
else
R = 1 ;
[0:0] := if(<0>R[1]==0) then
R = 0
else
R = 1 }

initialize phi {[0:Nr-1] := amp*r*exp(-(r-cent)^d/sigma^d) }
initialize Phi {[0:Nr-1] := amp*r*exp(-(r-cent)^d/sigma^d)*sigma^d*((-(r-cent))^d
*d/(r-cent) )/sigma^(2*d) + amp*exp(-(r-cent)^d/sigma^d) }
initialize Pi {[0:Nr-1] := Phi }
initialize Ktt {[0:Nr-1] := 2*M*(r+2*M)/(r*(r+2*M))^(3/2)}
initialize a {[0:Nr-1] := sqrt((r+2*M)/r)}
initialize beta {[0:Nr-1] := 2*M/(r+2*M)}
initialize Krr {[0:Nr-1] := -2*M*(r+M)/(r*(r+2*M))^(3/2)}
initialize dmdr {[0:Nr-1] := 4*PI*r^2*((Phi^2+Pi^2)/(2*a^2) + r*Ktt*Phi*Pi/a)}
initialize mass {[0:Nr-1] := M}
initialize ah {[0:Nr-1] := a*r*Ktt}
initialize R {[0:Nr-1] := if(ah>=1.0) then 0 else 1 }
initialize mc { [0:0] :=(D_FW02(Ktt,r) + (Ktt - Krr)/r - 4*PI*Phi*Pi/a);
[1:Nr-2] :=(D_LF(Ktt,r) + (Ktt - Krr)/r - 4*PI*Phi*Pi/a);
[Nr-1:Nr-1] :=(D_BW(Ktt,r) + (Ktt - Krr)/r - 4*PI*Phi*Pi/a) }
initialize hc { [0:0] := (D_FW02(a,r) - 1/(2*r)*(a-a^3) - 1/2*r*(4*PI*a*(Phi^2 + Pi^2) -
a^3*Ktt*(Ktt+2*Krr)));
[1:Nr-2] := (D_LF(a,r) - 1/(2*r)*(a-a^3) - 1/2*r*(4*PI*a*(Phi^2 + Pi^2) -
a^3*Ktt*(Ktt+2*Krr)));
[Nr-1:Nr-1] := (D_BW(a,r) - 1/(2*r)*(a-a^3) - 1/2*r*(4*PI*a*(Phi^2 + Pi^2) -
a^3*Ktt*(Ktt+2*Krr))) }

auto initialize phi,Phi,Pi
init.frag init initialize
Ktt, Krr, a, beta, dmdr, mass
header
Phi, Pi, Ktt, Krr, a, beta, dmdr, mass, r, dr, PI, M

auto initialize ah,R,mass2,hc,mc,Ricci

looper iterative

auto update Phi,Pi,phi,a,beta,Ktt,Krr
auto update dmdr, mass, ah, R, hc, mc, mass2, Ricci
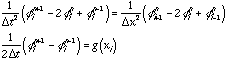
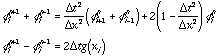
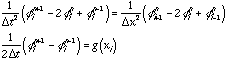
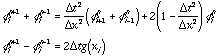