|
Brans-Dicke
/ Massless Scalar Field Critical Solutions M.W. Choptuik and S.L. Liebling, August 2007 |
| Description of Numerical Experiments |
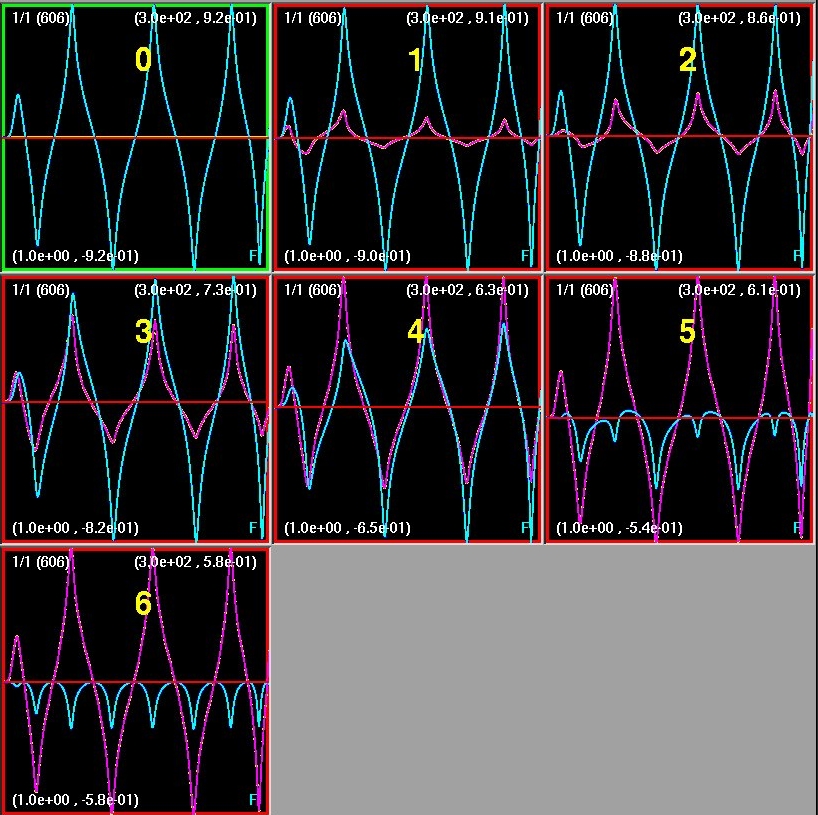
| Screenshot 1: Central value of fields in
near critical evolutions with varying contributions of Brans-Dicke
(cyan) and massless (magenta) scalars. |
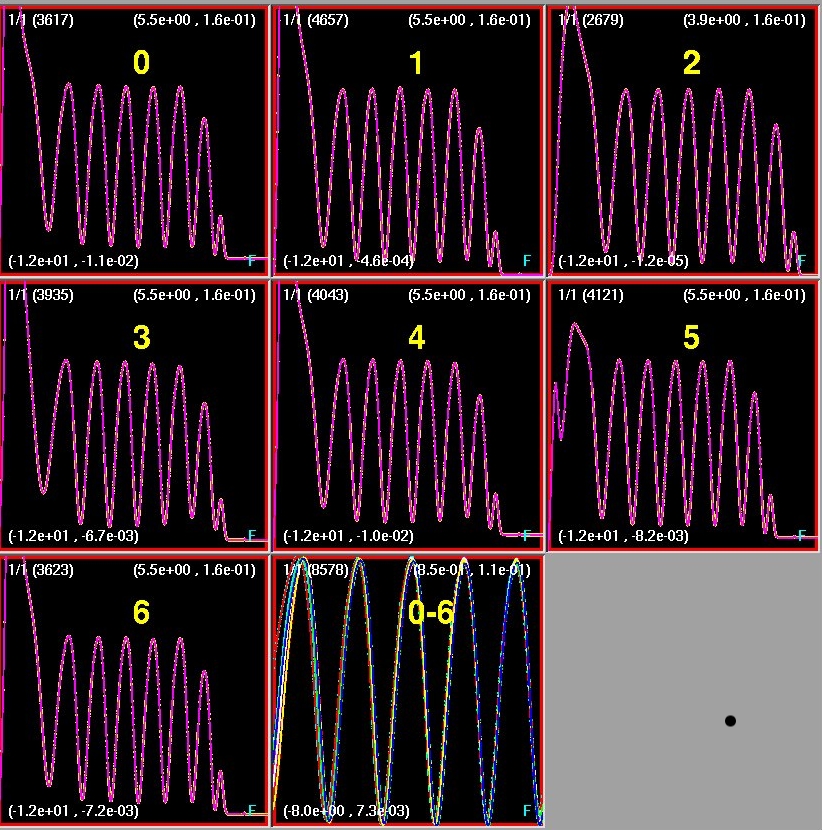
| Screenshot 2: Late time snapshot of
dm/dr(t**,r) for near critical evolutions as above. |
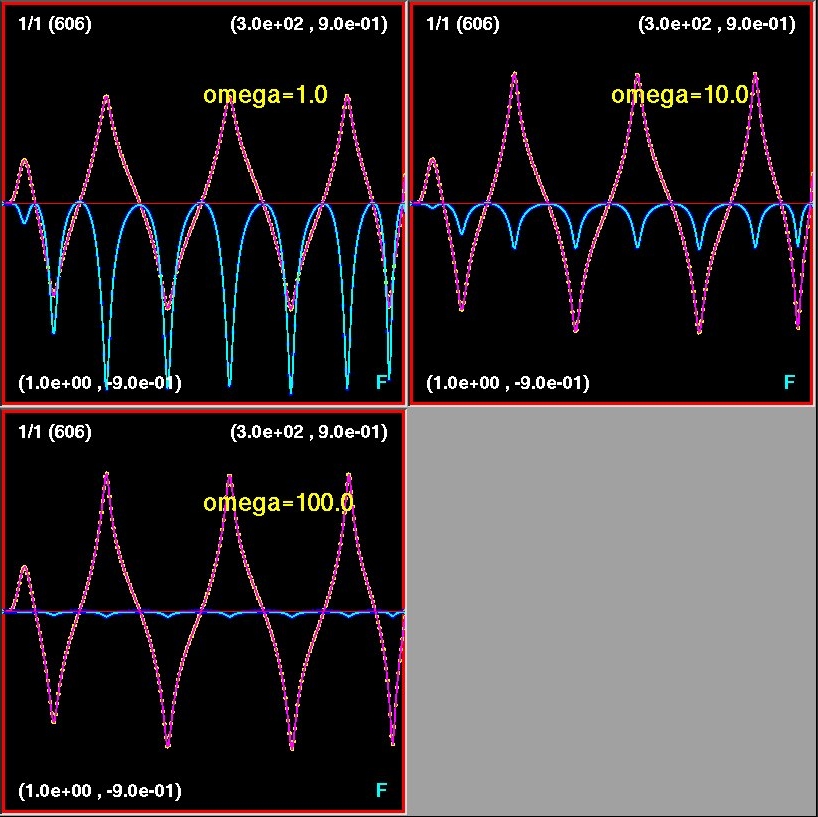
| Screenshot 3: Central value of fields in near critical evolutions, all with xi(0,t) = 0, and with omega varying as indcated. Cyan: Brans-Dicke field. Magenta: Massless scalar field. Red: x-axis |
| Maintained by choptuik@phas.ubc.ca. Supported by CIFAR, NSERC, CFI, BCKDF and UBC. |