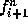Derivative operators are operators which act on grid functions. They are used for turning differential equations into finite difference equations. Here is a declaration for a forward difference operator:
operator D_FW(f,r) := (<0>f[1] - <0>f[0])/dr
Whenever an operator is used in an expression (see section
1.12), the operator is replaced by its definition. The name
f is arbitrary. It simply shows where the expression goes in the
definition. For instance, if D_FW(3*A+B,r) appeared in an expression,
the f's in the right hand side would be replaced by 3*A+B.
The notation <0>f[1] is interpreted as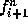 
,
that is, f at the nth time level and i+1st grid position. The <>[] is
really an operator which acts on expressions as follows:
<a>f[b]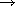 
f if f is a number or parameter or time coordinate
<a>f[b] 
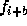if f is a spatial coordinate
<a>f[b]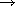 
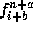if f is a grid function
Three dimensional forward difference operators would look like this:
operator D_FW(f,x) := (<0>f[1][0][0] - <0>f[0][0][0])/dx operator D_FW(f,y) := (<0>f[0][1][0] - <0>f[0][0][0])/dy operator D_FW(f,z) := (<0>f[0][0][1] - <0>f[0][0][0])/dz
Operator definitions can be nested as in:
operator D_FW(f,r) := (<0>f[1] - <0>f[0])/dr operator D_BW(f,r) := (<0>f[0] - <0>f[-1])/dr operator D_CN1(f,r,r) := D_BW(D_FW(<0>f[0],r),r) operator D_CN2(f,r,r) := D_BW(D_FW(<1>f[0],r),r)
As you can predict, the definition of D_CN1 will result in the
usual centered second derivative, namely
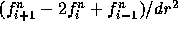, while the
definition of D_CN2 will result in the same thing applied at the
advanced time level, that is
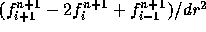. The list of
coordinate names after the f signifies with respect to which
coordinate(s) the derivative is taken.
Although operators are defined like derivatives and act as derivatives under certain circumstances (see section 1.12), they can be defined to perform other functions, such as the following definition which performs spatial averaging.
operator AVG(f,r) := (<0>f[1] + <0>f[0])/2
Because operators are internally treated as derivatives, even definitions such as this need the coordinate list.